Dalam topik ini, kita akan mempertimbangkan konsep matriks, serta jenis matriks. Memandangkan terdapat banyak istilah dalam topik ini, saya akan menambah ringkasan untuk memudahkan menavigasi bahan.
Definisi matriks dan unsurnya. Notasi.
Matriks ialah jadual dengan $m$ baris dan $n$ lajur. Unsur-unsur matriks boleh menjadi objek yang mempunyai sifat yang sangat pelbagai: nombor, pembolehubah, atau, sebagai contoh, matriks lain. Contohnya, matriks $\left(\begin(array) (cc) 5 & 3 \\ 0 & -87 \\ 8 & 0 \end(array) \right)$ mempunyai 3 baris dan 2 lajur; unsurnya ialah integer. Matriks $\left(\begin(array) (cccc) a & a^9+2 & 9 & \sin x \\ -9 & 3t^2-4 & u-t & 8\end(array) \right)$ mengandungi 2 baris dan 4 lajur.
Cara yang berbeza untuk menulis matriks: tunjukkan\sembunyikan
Matriks boleh ditulis bukan sahaja dalam kurungan bulat, tetapi juga dalam kurungan lurus persegi atau berganda. Di bawah ialah matriks yang sama dalam tatatanda yang berbeza:
$$ \left(\begin(array) (cc) 5 & 3 \\ 0 & -87 \\ 8 & 0 \end(array) \right);\;\; \left[ \begin(array) (cc) 5 & 3 \\ 0 & -87 \\ 8 & 0 \end(array) \right]; \;\; \left \Vert \begin(array) (cc) 5 & 3 \\ 0 & -87 \\ 8 & 0 \end(array) \right \Vert $$
Produk $m\times n$ dipanggil saiz matriks. Sebagai contoh, jika matriks mengandungi 5 baris dan 3 lajur, maka satu menyebut tentang matriks $5\kali 3$. Matriks $\left(\begin(array)(cc) 5 & 3\\0 & -87\\8 & 0\end(array)\right)$ mempunyai saiz $3 \times 2$.
Matriks biasanya dilambangkan dengan huruf besar abjad Latin: $A$, $B$, $C$, dan seterusnya. Contohnya, $B=\left(\begin(array) (ccc) 5 & 3 \\ 0 & -87 \\ 8 & 0 \end(array) \right)$. Penomboran baris pergi dari atas ke bawah; lajur - dari kiri ke kanan. Sebagai contoh, baris pertama matriks $B$ mengandungi unsur 5 dan 3, dan lajur kedua mengandungi unsur 3, -87, 0.
Unsur matriks biasanya dilambangkan dengan huruf kecil. Contohnya, unsur-unsur matriks $A$ dilambangkan dengan $a_(ij)$. Indeks berganda $ij$ mengandungi maklumat tentang kedudukan unsur dalam matriks. Nombor $i$ ialah nombor baris, dan nombor $j$ ialah nombor lajur, di persimpangan di mana unsur $a_(ij)$ terletak. Contohnya, pada persilangan baris kedua dan lajur kelima matriks $A=\left(\begin(array) (cccccc) 51 & 37 & -9 & 0 & 9 & 97 \\ 1 & 2 & 3 & 41 & 59 & 6 \ \ -17 & -15 & -13 & -11 & -8 & -5 \\ 52 & 31 & -4 & -1 & 17 & 90 \end(array) \right)$ elemen $ a_(25)= $59:
Begitu juga, di persimpangan baris pertama dan lajur pertama, kita mempunyai elemen $a_(11)=51$; di persimpangan baris ketiga dan lajur kedua - elemen $a_(32)=-15$ dan seterusnya. Ambil perhatian bahawa $a_(32)$ dibaca sebagai "a tiga dua" tetapi bukan "tiga puluh dua".
Untuk sebutan singkatan bagi matriks $A$, yang saiznya bersamaan dengan $m\times n$, notasi $A_(m\times n)$ digunakan. Notasi berikut sering digunakan:
$$ A_(m\times(n))=(a_(ij)) $$
Di sini $(a_(ij))$ menunjukkan penetapan unsur-unsur matriks $A$, i.e. mengatakan bahawa unsur-unsur matriks $A$ dilambangkan sebagai $a_(ij)$. Dalam bentuk dikembangkan, matriks $A_(m\times n)=(a_(ij))$ boleh ditulis seperti berikut:
$$ A_(m\times n)=\left(\begin(array)(cccc) a_(11) & a_(12) & \ldots & a_(1n) \\ a_(21) & a_(22) & \ldots & a_(2n) \\ \ldots & \ldots & \ldots & \ldots \\ a_(m1) & a_(m2) & \ldots & a_(mn) \end(array) \kanan) $$
Mari kita perkenalkan istilah lain - matriks yang sama.
Dua matriks yang sama saiz $A_(m\times n)=(a_(ij))$ dan $B_(m\times n)=(b_(ij))$ dipanggil sama rata jika elemen sepadan mereka adalah sama, i.e. $a_(ij)=b_(ij)$ untuk semua $i=\overline(1,m)$ dan $j=\overline(1,n)$.
Penjelasan untuk entri $i=\overline(1,m)$: show\hide
Entri "$i=\overline(1,m)$" bermaksud parameter $i$ berubah daripada 1 kepada m. Sebagai contoh, entri $i=\overline(1,5)$ mengatakan bahawa parameter $i$ mengambil nilai 1, 2, 3, 4, 5.
Jadi, untuk kesamaan matriks, dua syarat diperlukan: kebetulan saiz dan kesamaan unsur yang sepadan. Sebagai contoh, matriks $A=\left(\begin(array)(cc) 5 & 3\\0 & -87\\8 & 0\end(array)\right)$ tidak sama dengan matriks $B=\left(\ begin(array)(cc) 8 & -9\\0 & -87 \end(array)\kanan)$ kerana matriks $A$ ialah $3\kali 2$ dan matriks $B$ ialah $2\kali 2$. Juga matriks $A$ tidak sama dengan matriks $C=\left(\begin(array)(cc) 5 & 3\\98 & -87\\8 & 0\end(array)\kanan) $ kerana $a_( 21)\neq c_(21)$ (iaitu $0\neq 98$). Tetapi untuk matriks $F=\left(\begin(array)(cc) 5 & 3\\0 & -87\\8 & 0\end(array)\right)$, kita boleh menulis $A dengan selamat =F$ kerana kedua-dua saiz dan unsur yang sepadan bagi matriks $A$ dan $F$ bertepatan.
Contoh #1
Tentukan saiz matriks $A=\left(\begin(array) (ccc) -1 & -2 & 1 \\ 5 & 9 & -8 \\ -6 & 8 & 23 \\ 11 & -12 & -5 \ \ 4 & 0 & -10 \\ \end(array) \kanan)$. Nyatakan apakah elemen $a_(12)$, $a_(33)$, $a_(43)$ bersamaan.
Matriks ini mengandungi 5 baris dan 3 lajur, jadi saiznya ialah $5\kali 3$. Notasi $A_(5\times 3)$ juga boleh digunakan untuk matriks ini.
Elemen $a_(12)$ berada di persimpangan baris pertama dan lajur kedua, jadi $a_(12)=-2$. Unsur $a_(33)$ berada di persimpangan baris ketiga dan lajur ketiga, jadi $a_(33)=23$. Unsur $a_(43)$ berada di persimpangan baris keempat dan lajur ketiga, jadi $a_(43)=-5$.
Jawab: $a_(12)=-2$, $a_(33)=23$, $a_(43)=-5$.
Jenis matriks bergantung pada saiznya. pepenjuru utama dan sisi. Jejak matriks.
Biarkan beberapa matriks $A_(m\kali n)$ diberikan. Jika $m=1$ (matriks terdiri daripada satu baris), maka matriks yang diberikan dipanggil baris matriks. Jika $n=1$ (matriks terdiri daripada satu lajur), maka matriks sedemikian dipanggil matriks lajur. Contohnya, $\left(\begin(array) (ccccc) -1 & -2 & 0 & -9 & 8 \end(array) \right)$ ialah matriks baris dan $\left(\begin(array ) (c) -1 \\ 5 \\ 6 \end(array) \right)$ - matriks lajur.
Jika keadaan $m\neq n$ adalah benar untuk matriks $A_(m\times n)$ (iaitu, bilangan baris tidak sama dengan bilangan lajur), maka sering dikatakan bahawa $A$ ialah matriks segi empat tepat. Sebagai contoh, matriks $\left(\begin(array) (cccc) -1 & -2 & 0 & 9 \\ 5 & 9 & 5 & 1 \end(array) \right)$ mempunyai saiz $2\times 4 $, mereka. mengandungi 2 baris dan 4 lajur. Oleh kerana bilangan baris tidak sama dengan bilangan lajur, matriks ini adalah segi empat tepat.
Jika keadaan $m=n$ adalah benar untuk matriks $A_(m\times n)$ (iaitu, bilangan baris adalah sama dengan bilangan lajur), maka $A$ dikatakan sebagai matriks segi empat sama bagi pesanan $n$. Contohnya, $\left(\begin(array) (cc) -1 & -2 \\ 5 & 9 \end(array) \right)$ ialah matriks segi empat sama tertib kedua; $\left(\begin(array) (ccc) -1 & -2 & 9 \\ 5 & 9 & 8 \\ 1 & 0 & 4 \end(array) \right)$ ialah matriks segi empat sama tertib ke-3. Secara umum, matriks segi empat sama $A_(n\times n)$ boleh ditulis seperti berikut:
$$ A_(n\times n)=\left(\begin(array)(cccc) a_(11) & a_(12) & \ldots & a_(1n) \\ a_(21) & a_(22) & \ldots & a_(2n) \\ \ldots & \ldots & \ldots & \ldots \\ a_(n1) & a_(n2) & \ldots & a_(nn) \end(array) \kanan) $$
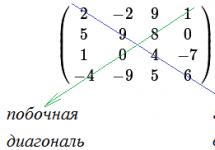
Unsur $a_(11)$, $a_(22)$, $\ldots$, $a_(nn)$ dikatakan berada pada pepenjuru utama matriks $A_(n\times n)$. Unsur-unsur ini dipanggil unsur pepenjuru utama(atau hanya unsur pepenjuru). Unsur $a_(1n)$, $a_(2 \; n-1)$, $\ldots$, $a_(n1)$ dihidupkan sisi (sekunder) pepenjuru; mereka dipanggil unsur pepenjuru sekunder. Contohnya, untuk matriks $C=\left(\begin(array)(cccc)2&-2&9&1\\5&9&8& 0\\1& 0 & 4 & -7 \\ -4 & -9 & 5 & 6\end( array) \right)$ kita ada:
Unsur $c_(11)=2$, $c_(22)=9$, $c_(33)=4$, $c_(44)=6$ ialah unsur pepenjuru utama; unsur $c_(14)=1$, $c_(23)=8$, $c_(32)=0$, $c_(41)=-4$ ialah unsur pepenjuru sekunder.
Jumlah unsur pepenjuru utama dipanggil diikuti dengan matriks dan dilambangkan dengan $\Tr A$ (atau $\Sp A$):
$$ \Tr A=a_(11)+a_(22)+\ldots+a_(nn) $$
Contohnya, untuk matriks $C=\left(\begin(array) (cccc) 2 & -2 & 9 & 1\\5 & 9 & 8 & 0\\1 & 0 & 4 & -7\\- 4 & -9 & 5 & 6 \end(array)\kanan)$ kita ada:
$$ \Tr C=2+9+4+6=21. $$
Konsep unsur pepenjuru juga digunakan untuk matriks bukan segi empat sama. Contohnya, untuk matriks $B=\left(\begin(array) (ccccc) 2 & -2 & 9 & 1 & 7 \\ 5 & -9 & 8 & 0 & -6 \\ 1 & 0 & 4 & - 7 & -6 \end(array) \right)$ unsur pepenjuru utama ialah $b_(11)=2$, $b_(22)=-9$, $b_(33)=4$.
Jenis matriks bergantung pada nilai unsurnya.
Jika semua elemen matriks $A_(m\times n)$ adalah sama dengan sifar, maka matriks sedemikian dipanggil null dan biasanya dilambangkan dengan huruf $O$. Contohnya, $\left(\begin(array) (cc) 0 & 0 \\ 0 & 0 \\ 0 & 0 \end(array) \right)$, $\left(\begin(array) (ccc) 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end(array) \right)$ ialah matriks sifar.
Pertimbangkan beberapa baris bukan sifar bagi matriks $A$, i.e. rentetan yang mengandungi sekurang-kurangnya satu unsur bukan sifar. unsur peneraju daripada rentetan bukan sifar, mari kita panggil ia unsur bukan sifar yang pertama (mengira dari kiri ke kanan). Sebagai contoh, pertimbangkan matriks berikut:
$$W=\left(\begin(array)(cccc) 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 12\\ 0 & -9 & 5 & 9 \end(array)\kanan)$ $
Dalam baris kedua, elemen keempat akan mendahului, i.e. $w_(24)=12$, dan dalam baris ketiga elemen utama akan menjadi elemen kedua, i.e. $w_(32)=-9$.
Matriks $A_(m\times n)=\left(a_(ij)\kanan)$ dipanggil melangkah jika ia memenuhi dua syarat:
- Baris nol, jika ada, terletak di bawah semua baris bukan nol.
- Bilangan unsur utama rentetan bukan sifar membentuk urutan yang semakin meningkat, i.e. jika $a_(1k_1)$, $a_(2k_2)$, ..., $a_(rk_r)$ ialah unsur utama bagi baris bukan sifar matriks $A$, maka $k_1\lt(k_2)\lt\ldots\ lt( k_r)$.
Contoh matriks langkah:
$$ \left(\begin(array)(cccccc) 0 & 0 & 2 & 0 & -4 & 1\\ 0 & 0 & 0 & 0 & -9 & 0\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 \end(array)\kanan);\; \left(\begin(array)(cccc) 5 & -2 & 2 & -8\\ 0 & 4 & 0 & 0\\ 0 & 0 & 0 & -10 \end(array)\kanan). $$
Sebagai perbandingan: matriks $Q=\left(\begin(array)(ccccc) 2 & -2 & 0 & 1 & 9\\0 & 0 & 0 & 7 & 9\\0 & -5 & 0 & 10 & 6\end(array)\right)$ bukan matriks langkah, kerana syarat kedua dalam takrifan matriks langkah dilanggar. Unsur utama dalam baris kedua dan ketiga $q_(24)=7$ dan $q_(32)=10$ bernombor $k_2=4$ dan $k_3=2$. Untuk matriks langkah, syarat $k_2\lt(k_3)$ mesti dipenuhi, yang dilanggar dalam kes ini. Saya perhatikan bahawa jika kita menukar baris kedua dan ketiga, kita mendapat matriks berperingkat: $\left(\begin(array)(ccccc) 2 & -2 & 0 & 1 & 9\\0 & -5 & 0 & 10 & 6 \\0 & 0 & 0 & 7 & 9\end(array)\kanan)$.
Matriks langkah dipanggil trapezoid atau trapezoid, jika elemen utama $a_(1k_1)$, $a_(2k_2)$, ..., $a_(rk_r)$ memenuhi syarat $k_1=1$, $k_2=2$,..., $k_r = r$, i.e. unsur pepenjuru mendahului. Secara umum, matriks trapezoid boleh ditulis seperti berikut:
$$ A_(m\times(n)) =\left(\mula(array) (cccccc) a_(11) & a_(12) & \ldots & a_(1r) & \ldots & a_(1n)\\ 0 & a_(22) & \ldots & a_(2r) & \ldots & a_(2n)\\ \ldots & \ldots & \ldots & \ldots & \ldots & \ldots\\ 0 & 0 & \ldots & a_(rr) & \ldots & a_(rn)\\ 0 & 0 & \ldots & 0 & \ldots & 0\\ \ldots & \ldots & \ldots & \ldots & \ldots & \ldots\\ 0 & 0 & \ldots & 0 & \ldots & 0 \end(array)\kanan) $$
Contoh matriks trapezoid:
$$ \left(\begin(array)(cccccc) 4 & 0 & 2 & 0 & -4 & 1\\ 0 & -2 & 0 & 0 & -9 & 0\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 \end(array)\kanan);\; \left(\begin(array)(cccc) 5 & -2 & 2 & -8\\ 0 & 4 & 0 & 0\\ 0 & 0 & -3 & -10 \end(array)\kanan). $$
Mari kita berikan beberapa lagi definisi untuk matriks segi empat sama. Jika semua elemen matriks persegi yang terletak di bawah pepenjuru utama adalah sama dengan sifar, maka matriks sedemikian dipanggil matriks segi tiga atas. Contohnya, $\left(\begin(array) (cccc) 2 & -2 & 9 & 1 \\ 0 & 9 & 8 & 0 \\ 0 & 0 & 4 & -7 \\ 0 & 0 & 0 & 6 \end(array) \right)$ - matriks segi tiga atas. Perhatikan bahawa takrifan matriks segi tiga atas tidak menyatakan apa-apa tentang nilai unsur yang terletak di atas pepenjuru utama atau pada pepenjuru utama. Mereka mungkin sifar atau tidak, tidak mengapa. Contohnya, $\left(\begin(array) (ccc) 0 & 0 & 9 \\ 0 & 0 & 0\\ 0 & 0 & 0 \end(array) \right)$ juga merupakan matriks segi tiga atas.
Jika semua elemen matriks segi empat sama yang terletak di atas pepenjuru utama adalah sama dengan sifar, maka matriks sedemikian dipanggil matriks segitiga bawah. Contohnya, $\left(\begin(array) (cccc) 3 & 0 & 0 & 0 \\ -5 & 1 & 0 & 0 \\ 8 & 2 & 1 & 0 \\ 5 & 4 & 0 & 6 \ end(array) \right)$ - matriks segi tiga bawah. Ambil perhatian bahawa takrifan matriks segi tiga yang lebih rendah tidak menyatakan apa-apa tentang nilai unsur di bawah atau pada pepenjuru utama. Mereka mungkin batal atau tidak, tidak mengapa. Contohnya, $\left(\begin(array) (ccc) -5 & 0 & 0 \\ 0 & 0 & 0\\ 0 & 0 & 9 \end(array) \right)$ dan $\left(\ mula (tatasusunan) (ccc) 0 & 0 & 0 \\ 0 & 0 & 0\\ 0 & 0 & 0 \end(array) \kanan)$ juga adalah matriks segi tiga yang lebih rendah.
Matriks segi empat sama dipanggil pepenjuru jika semua elemen matriks ini yang tidak berada pada pepenjuru utama adalah sama dengan sifar. Contoh: $\left(\begin(array) (cccc) 3 & 0 & 0 & 0 \\ 0 & -2 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 6 \ end(array)\kanan)$. Unsur-unsur pada pepenjuru utama boleh menjadi apa-apa sahaja (sama dengan sifar atau tidak) - ini tidak penting.
Matriks pepenjuru dipanggil bujang jika semua elemen matriks ini terletak pada pepenjuru utama adalah sama dengan 1. Contohnya, $\left(\begin(array) (cccc) 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end(array)\kanan)$ - matriks identiti tertib ke-4; $\left(\begin(array) (cc) 1 & 0 \\ 0 & 1 \end(array)\right)$ ialah matriks identiti tertib kedua.
Perhatikan bahawa unsur-unsur matriks boleh bukan sahaja nombor. Bayangkan anda sedang menerangkan buku yang ada di rak buku anda. Biarkan rak anda teratur dan semua buku diletakkan di tempat yang ditetapkan dengan ketat. Jadual yang akan mengandungi perihalan perpustakaan anda (mengikut rak dan urutan buku di rak) juga akan menjadi matriks. Tetapi matriks sedemikian tidak akan menjadi berangka. Contoh yang lain. Daripada nombor, terdapat fungsi yang berbeza, bersatu di antara mereka oleh beberapa pergantungan. Jadual yang terhasil juga akan dipanggil matriks. Dengan kata lain, Matriks ialah sebarang jadual segi empat tepat yang terdiri daripada homogen elemen. Di sini dan di bawah kita akan bercakap tentang matriks yang terdiri daripada nombor.
Daripada kurungan, matriks ditulis menggunakan kurungan segi empat sama atau garis menegak berganda lurus.
 |
(2.1*) |
Definisi 2. Jika dalam ungkapan(1) m = n , kemudian mereka bercakap tentang matriks segi empat sama, bagaimana jika , sesuatu tentang segi empat tepat.
Bergantung pada nilai m dan n, terdapat beberapa jenis matriks khas:
Ciri yang paling penting segi empat sama matriks adalah miliknya penentu atau penentu, yang terdiri daripada unsur matriks dan dilambangkan
Jelas sekali, D E =1 ; .
Definisi 3. Sekiranya , kemudian matriks A dipanggil tidak merosot atau tidak istimewa.
Definisi 4. Sekiranya detA = 0 , kemudian matriks A dipanggil merosot atau istimewa.
Definisi 5. Dua matriks A dan B dipanggil sama rata dan menulis A=B jika mereka mempunyai dimensi yang sama dan unsur yang sepadan adalah sama, i.e..
Sebagai contoh, matriks dan adalah sama, kerana ia adalah sama dalam saiz dan setiap elemen satu matriks adalah sama dengan elemen sepadan matriks yang lain. Tetapi matriks tidak boleh dipanggil sama, walaupun penentu kedua-dua matriks adalah sama, dan dimensi matriks adalah sama, tetapi tidak semua elemen di tempat yang sama adalah sama. Matriks adalah berbeza kerana ia mempunyai saiz yang berbeza. Matriks pertama ialah 2x3 dan yang kedua 3x2. Walaupun bilangan elemen adalah sama - 6 dan elemen itu sendiri adalah sama 1, 2, 3, 4, 5, 6, tetapi mereka berada di tempat yang berbeza dalam setiap matriks. Tetapi matriks dan adalah sama, menurut Definisi 5.
Definisi 6. Jika kita menetapkan bilangan lajur matriks tertentu A dan bilangan barisnya yang sama, maka unsur-unsur di persilangan lajur dan baris yang ditentukan membentuk matriks segi empat sama n- urutan ke-, penentu yang mana dipanggil bawah umur k- matriks pesanan ke- A.
Contoh. Tulis tiga minor bagi susunan kedua matriks itu
Tiket 17:
Soalan 1: Definisi parabola. Terbitan persamaan:
Definisi. Parabola ialah satu set titik dalam satah, setiap satunya berada pada jarak yang sama dari titik tertentu, dipanggil fokus, dan dari garis lurus tertentu, dipanggil directrix dan tidak melalui fokus.
Mari kita letakkan asal koordinat di tengah-tengah antara fokus dan directrix.
Nilai p (jarak dari fokus ke directrix) dipanggil parameter parabola. Kami memperoleh persamaan kanonik parabola.
Daripada perhubungan geometri: AM = MF; AM = x + p/2;
MF2 = y2 + (x – p/2)2
(x + p/2)2 = y2 + (x – p/2)2
x2 + xp + p2/4 = y2 + x2 – xp + p2/4
Persamaan Arahan: x = -p/2.
Soalan 2: Teorem Cauchy:
Teorem: Biarkan fungsi dan boleh dibezakan pada selang dan berterusan untuk dan, lebih-lebih lagi, untuk semua . Kemudian terdapat satu titik dalam selang seperti itu
deria geometri : Teorem ini terdiri daripada fakta bahawa di dalamnya terdapat titik t 0 , cerun yang dikira dengan kesamaan:
Bukti.
Mari kita buktikan dahulu 
, iaitu pecahan di sebelah kiri formula masuk akal. Sesungguhnya, untuk perbezaan ini, kita boleh menulis formula untuk kenaikan terhingga:
pada beberapa. Tetapi di sebelah kanan formula ini, kedua-dua faktor adalah bukan sifar.
Untuk membuktikan teorem, kami memperkenalkan fungsi tambahan
Fungsi ini jelas boleh dibezakan untuk semua dan berterusan pada titik dan , kerana fungsi dan mempunyai sifat ini. Selain itu, adalah jelas bahawa untuk , kita memperoleh . Mari tunjukkan itu dan:
Oleh itu, fungsi itu memenuhi syarat teorem Rolle pada selang. Oleh itu, ada satu perkara seperti itu.
Kami kini mengira derivatif fungsi:
Kami dapat itu
dari mana kita memperoleh penegasan teorem:
Ulasan: Kita boleh mempertimbangkan fungsi dan koordinat titik yang bergerak pada satah, yang menerangkan garis yang menghubungkan titik permulaan dengan titik akhir. (Kemudian persamaan dan secara parametrik menetapkan beberapa pergantungan, graf yang merupakan garis.)
Rajah 5.6 Kord adalah selari dengan beberapa tangen kepada lengkung
Nisbah, kerana ia mudah dilihat dari lukisan, kemudian menetapkan cerun kord yang menghubungkan titik dan . Pada masa yang sama, mengikut formula untuk derivatif fungsi yang diberikan secara parametrik, kita mempunyai: 
. Jadi pecahan ialah kecerunan tangen kepada garis pada satu titik 
. Oleh itu, pernyataan teorem bermakna, dari sudut pandangan geometri, bahawa terdapat satu titik pada garis sedemikian rupa sehingga tangen yang dilukis pada titik ini adalah selari dengan kord yang menghubungkan titik ekstrem garis. Tetapi ini adalah pernyataan yang sama yang membentuk makna geometri teorem Lagrange. Hanya dalam teorem Lagrange garis diberikan oleh pergantungan yang jelas, dan dalam teorem Cauchy oleh pergantungan yang diberikan dalam bentuk parametrik.
Tiket 18:
Soalan 1: Konsep matriks. Klasifikasi matriks:
Definisi.
Matriks bersaiz mn, dengan m ialah bilangan baris, n ialah bilangan lajur, ialah jadual nombor yang disusun dalam susunan tertentu. Nombor ini dipanggil elemen matriks. Tempat setiap elemen ditentukan secara unik oleh bilangan baris dan lajur di persimpangan di mana ia terletak. Unsur matriks dilambangkan dengan aij, di mana i ialah nombor baris dan j ialah nombor lajur. A = 
Klasifikasi matriks:.
Matriks boleh mempunyai satu baris atau satu lajur. Secara umumnya, matriks bahkan boleh terdiri daripada satu elemen.
Definisi . Jika bilangan lajur matriks sama dengan bilangan baris (m=n), maka matriks itu dipanggil segi empat sama.
Definisi
. Lihat Matriks: 
= E dipanggil matriks identiti.
Definisi. Jika amn = anm , maka matriks dipanggil simetri. Contoh. - matriks simetri
Definisi
. Matriks pandangan segi empat sama 
dipanggil matriks pepenjuru
.
Soalan 2: Teorem Lagrange:
Teorem:
Biarkan fungsi boleh dibezakan pada selang dan berterusan pada titik dan . Kemudian ada satu perkara seperti itu 
deria geometri:
Mari kita berikan ilustrasi geometri teorem terlebih dahulu. Sambungkan titik akhir graf pada segmen dengan kord. Kenaikan terhingga dan 
ialah panjang kaki segi tiga, hipotenusnya ialah kord yang dilukis.
Rajah 5.5 Tangen pada satu titik adalah selari dengan kord
Nisbah kenaikan akhir dan ialah tangen bagi kecerunan kord. Teorem menyatakan bahawa tangen boleh dilukis kepada graf fungsi boleh dibezakan pada satu titik, yang akan selari dengan kord, iaitu, kecerunan tangen () akan sama dengan kecerunan kord (). Tetapi kehadiran tangen sedemikian jelas secara geometri.
Perhatikan bahawa kord yang dilukis menghubungkan titik-titik dan ialah graf bagi fungsi linear. Oleh kerana kecerunan fungsi linear ini jelas sama dengan 
, kemudian 
Bukti teorem Lagrange. Kami mengurangkan bukti penggunaan teorem Rolle. Untuk melakukan ini, kami memperkenalkan fungsi tambahan, iaitu,
perasan, itu 
dan (dengan membina fungsi ). Oleh kerana fungsi linear boleh dibezakan untuk semua , maka fungsi itu memenuhi semua sifat yang disenaraikan dalam keadaan teorem Rolle. Oleh itu, terdapat satu perkara yang Cheat Sheet pada Falsafah: Jawapan Tiket Peperiksaan Lembaran tipu >> Falsafah
katil bayi pada falsafah: jawapan kepada kertas peperiksaan... lukisan, arca dan seni bina, kerja pada matematik, biologi, geologi, anatomi dikhaskan untuk manusia ... disiplin diri, orientasikan diri anda kepada lebih tinggi matlamat. Idea utama Timur kuno ...
katil bayi pada Logik: Jawapan kepada Tiket Peperiksaan
Lembaran tipu >> FalsafahValery Vechkanov katil bayi pada ahli logik Vladimir Eduardovich Vechkanov katil bayi pada logik: ... pemikiran manusia. Fisiologi lebih tinggi aktiviti saraf mendedahkan secara semula jadi... fungsi proposisi digunakan secara meluas dalam matematik. Semua persamaan dengan satu...
katil bayi pada Ekonometrik (1)
Helaian tipu >> Ekonomistatistik; perangkaan ekonomi; lebih tinggi matematik. Bermakna. sumbangan kepada pembangunan... pada tahap sesak pada arah dan pada penjajaran analitikal. Oleh... berubah ke arah yang bertentangan. Oleh penjajaran analitikal: - hubungan linear...
Matriks ialah objek khas dalam matematik. Ia digambarkan dalam bentuk jadual segi empat tepat atau persegi, terdiri daripada bilangan baris dan lajur tertentu. Dalam matematik, terdapat pelbagai jenis matriks, berbeza dari segi saiz atau kandungan. Nombor baris dan lajurnya dipanggil pesanan. Objek ini digunakan dalam matematik untuk mengatur penulisan sistem persamaan linear dan mencari keputusannya dengan mudah. Persamaan menggunakan matriks diselesaikan menggunakan kaedah Carl Gauss, Gabriel Cramer, penambahan minor dan algebra, dan banyak cara lain. Kemahiran asas apabila bekerja dengan matriks adalah untuk mengurangkan kepada Walau bagaimanapun, pertama, mari kita fikirkan jenis matriks yang dibezakan oleh ahli matematik.
Jenis sifar
Semua komponen matriks jenis ini adalah sifar. Sementara itu, bilangan baris dan lajurnya berbeza sama sekali.
jenis persegi
Bilangan lajur dan baris jenis matriks ini adalah sama. Dalam erti kata lain, ia adalah jadual bentuk "persegi". Bilangan lajurnya (atau baris) dipanggil tertib. Kes khas ialah kewujudan matriks urutan kedua (matriks 2x2), urutan keempat (4x4), kesepuluh (10x10), ketujuh belas (17x17) dan seterusnya.
Vektor Lajur
Ini adalah salah satu jenis matriks yang paling mudah, mengandungi hanya satu lajur, yang merangkumi tiga nilai berangka. Ia mewakili beberapa sebutan bebas (nombor bebas daripada pembolehubah) dalam sistem persamaan linear.
Lihat serupa dengan yang sebelumnya. Terdiri daripada tiga elemen berangka, seterusnya disusun dalam satu baris.
Jenis pepenjuru
Nilai berangka dalam bentuk pepenjuru matriks hanya mengambil komponen pepenjuru utama (diserlahkan dalam warna hijau). Diagonal utama bermula dari elemen yang terletak di sudut kiri atas, dan berakhir dengan elemen di bahagian bawah kanan, masing-masing. Selebihnya komponen adalah sifar. Jenis pepenjuru hanyalah matriks segi empat sama dengan susunan tertentu. Di antara matriks bentuk pepenjuru, seseorang boleh memilih skalar. Semua komponennya mengambil nilai yang sama.
Subspesies matriks pepenjuru. Semua nilai berangkanya adalah unit. Menggunakan satu jenis jadual matriks, transformasi asasnya dilakukan atau didapati matriks songsang kepada yang asal.
Jenis kanonik
Bentuk kanonik matriks dianggap sebagai salah satu yang utama; pemutus kepadanya selalunya diperlukan untuk berfungsi. Bilangan baris dan lajur dalam matriks kanonik adalah berbeza, ia tidak semestinya tergolong dalam jenis segi empat sama. Ia agak serupa dengan matriks identiti, bagaimanapun, dalam kesnya, tidak semua komponen pepenjuru utama mengambil nilai yang sama dengan satu. Terdapat dua atau empat unit pepenjuru utama (semuanya bergantung pada panjang dan lebar matriks). Atau mungkin tiada unit langsung (maka ia dianggap sifar). Baki komponen jenis kanonik, serta unsur-unsur jenis pepenjuru dan unit, adalah sama dengan sifar.
jenis segi tiga
Salah satu jenis matriks yang paling penting digunakan semasa mencari penentunya dan semasa melakukan operasi mudah. Jenis segi tiga berasal dari jenis pepenjuru, jadi matriks juga persegi. Pandangan segi tiga matriks dibahagikan kepada segi tiga atas dan segitiga bawah.
Dalam matriks segi tiga atas (Rajah 1), hanya unsur-unsur yang berada di atas pepenjuru utama mengambil nilai yang sama dengan sifar. Komponen pepenjuru itu sendiri dan bahagian matriks di bawahnya mengandungi nilai berangka.
Dalam matriks segitiga bawah (Rajah 2), sebaliknya, unsur-unsur yang terletak di bahagian bawah matriks adalah sama dengan sifar.
Borang ini diperlukan untuk mencari pangkat matriks, serta untuk operasi asas padanya (bersama-sama dengan jenis segi tiga). Matriks langkah dinamakan sedemikian kerana ia mengandungi ciri "langkah" sifar (seperti yang ditunjukkan dalam rajah). Dalam jenis bertingkat, pepenjuru sifar terbentuk (tidak semestinya yang utama), dan semua elemen di bawah pepenjuru ini juga mempunyai nilai yang sama dengan sifar. Prasyarat adalah yang berikut: jika terdapat baris sifar dalam matriks langkah, maka baris yang tinggal di bawahnya juga tidak mengandungi nilai berangka.
Oleh itu, kami telah mempertimbangkan jenis matriks yang paling penting yang diperlukan untuk bekerja dengannya. Sekarang mari kita berurusan dengan tugas menukar matriks ke dalam bentuk yang diperlukan.
Pengurangan kepada bentuk segi tiga
Bagaimana untuk membawa matriks kepada bentuk segi tiga? Selalunya, dalam tugasan, anda perlu menukar matriks kepada bentuk segi tiga untuk mencari penentunya, atau dipanggil penentu. Apabila melakukan prosedur ini, adalah sangat penting untuk "memelihara" pepenjuru utama matriks, kerana penentu matriks segi tiga adalah tepat hasil daripada komponen pepenjuru utamanya. Izinkan saya juga mengingatkan anda tentang kaedah alternatif untuk mencari penentu. Penentu jenis segi empat sama didapati menggunakan formula khas. Sebagai contoh, anda boleh menggunakan kaedah segitiga. Untuk matriks lain, kaedah penguraian mengikut baris, lajur, atau elemennya digunakan. Anda juga boleh menggunakan kaedah minor dan pelengkap algebra bagi matriks.
Marilah kita menganalisis secara terperinci proses membawa matriks kepada bentuk segi tiga menggunakan contoh beberapa tugasan.
Latihan 1
Ia adalah perlu untuk mencari penentu matriks yang dibentangkan, menggunakan kaedah membawanya ke bentuk segi tiga.
Matriks yang diberikan kepada kami ialah matriks segi empat sama tertib ketiga. Oleh itu, untuk mengubahnya menjadi bentuk segi tiga, kita perlu menghilangkan dua komponen lajur pertama dan satu komponen kedua.
Untuk membawanya ke bentuk segi tiga, kami memulakan transformasi dari sudut kiri bawah matriks - dari nombor 6. Untuk menjadikannya sifar, kami mendarabkan baris pertama dengan tiga dan menolaknya dari baris terakhir.
Penting! Baris atas tidak berubah, tetapi tetap sama seperti dalam matriks asal. Anda tidak perlu menulis rentetan empat kali ganda daripada rentetan asal. Tetapi nilai baris yang komponennya perlu ditetapkan kepada sifar sentiasa berubah.
Hanya nilai terakhir yang tinggal - elemen baris ketiga lajur kedua. Ini adalah nombor (-1). Untuk mengubahnya kepada sifar, tolak baris kedua daripada baris pertama.
Mari semak:
detA = 2 x (-1) x 11 = -22.
Oleh itu, jawapan kepada tugas: -22.
Tugasan 2
Ia adalah perlu untuk mencari penentu matriks dengan membawanya kepada bentuk segi tiga.
Matriks yang dibentangkan tergolong dalam jenis segi empat sama dan merupakan matriks tertib keempat. Ini bermakna bahawa adalah perlu untuk menghilangkan tiga komponen lajur pertama, dua komponen lajur kedua, dan satu komponen lajur ketiga.
Mari kita mulakan menghantarnya dari elemen yang terletak di sudut kiri bawah - dari nombor 4. Kita perlu menukar nombor ini kepada sifar. Cara paling mudah untuk melakukan ini ialah dengan mendarab baris atas dengan empat dan kemudian menolaknya daripada baris keempat. Mari kita tuliskan hasil peringkat pertama transformasi.
Jadi, komponen baris keempat ditetapkan kepada sifar. Mari kita beralih ke elemen pertama baris ketiga, ke nombor 3. Kami melakukan operasi yang serupa. Darab dengan tiga baris pertama, tolak daripada baris ketiga dan tulis hasilnya.
Kami berjaya menetapkan kepada sifar semua komponen lajur pertama matriks segi empat sama ini, kecuali nombor 1, unsur pepenjuru utama yang tidak memerlukan transformasi. Sekarang adalah penting untuk mengekalkan sifar yang terhasil, jadi kami akan melakukan transformasi dengan baris, bukan lajur. Mari kita beralih ke lajur kedua matriks yang dibentangkan.
Mari kita mulakan dari bawah sekali lagi - dari elemen lajur kedua baris terakhir. Ini adalah nombor (-7). Walau bagaimanapun, dalam kes ini adalah lebih mudah untuk bermula dengan nombor (-1) - elemen lajur kedua baris ketiga. Untuk mengubahnya kepada sifar, tolak baris kedua daripada baris ketiga. Kemudian kami mendarabkan baris kedua dengan tujuh dan menolaknya dari yang keempat. Kami mendapat sifar dan bukannya elemen yang terletak di baris keempat lajur kedua. Sekarang mari kita beralih ke lajur ketiga.
Dalam lajur ini, kita perlu bertukar kepada sifar hanya satu nombor - 4. Ini mudah dilakukan: hanya tambahkan yang ketiga pada baris terakhir dan lihat sifar yang kita perlukan.
Selepas semua transformasi, kami membawa matriks yang dicadangkan kepada bentuk segi tiga. Sekarang, untuk mencari penentunya, anda hanya perlu mendarab unsur-unsur yang terhasil daripada pepenjuru utama. Kita mendapatkan: detA = 1 x (-1) x (-4) x 40 = 160. Oleh itu, penyelesaiannya ialah nombor 160.
Jadi, kini persoalan untuk membawa matriks kepada bentuk segi tiga tidak akan menyukarkan anda.
Pengurangan kepada bentuk berperingkat
Untuk operasi asas pada matriks, bentuk berperingkat adalah kurang "diminta" daripada segi tiga. Ia paling biasa digunakan untuk mencari kedudukan matriks (iaitu, bilangan baris bukan sifarnya) atau untuk menentukan baris bersandar dan bebas secara linear. Walau bagaimanapun, pandangan bertingkat matriks adalah lebih serba boleh, kerana ia sesuai bukan sahaja untuk jenis segi empat sama, tetapi untuk orang lain.
Untuk mengurangkan matriks kepada bentuk berperingkat, anda perlu mencari penentunya terlebih dahulu. Untuk ini, kaedah di atas sesuai. Tujuan mencari penentu adalah untuk mengetahui sama ada ia boleh ditukar kepada matriks langkah. Jika penentu lebih besar atau kurang daripada sifar, maka anda boleh meneruskan tugas dengan selamat. Jika ia sama dengan sifar, ia tidak akan berfungsi untuk mengurangkan matriks kepada bentuk berperingkat. Dalam kes ini, anda perlu menyemak sama ada terdapat sebarang ralat dalam rekod atau dalam transformasi matriks. Sekiranya tidak ada ketidaktepatan sedemikian, tugas itu tidak dapat diselesaikan.
Mari kita pertimbangkan cara untuk membawa matriks ke bentuk berperingkat menggunakan contoh beberapa tugasan.
Latihan 1. Cari pangkat jadual matriks yang diberi.
Di hadapan kita ialah matriks segi empat sama tertib ketiga (3x3). Kita tahu bahawa untuk mencari pangkat, perlu mengurangkannya kepada bentuk berperingkat. Oleh itu, kita perlu mencari penentu matriks terlebih dahulu. Mari gunakan kaedah segitiga: detA = (1 x 5 x 0) + (2 x 1 x 2) + (6 x 3 x 4) - (1 x 1 x 4) - (2 x 3 x 0) - (6 x 5 x 2) = 12.
Penentu = 12. Ia lebih besar daripada sifar, yang bermaksud bahawa matriks boleh dikurangkan kepada bentuk bertingkat. Mari kita mula mengubahnya.
Mari kita mulakan dengan elemen lajur kiri baris ketiga - nombor 2. Kami mendarabkan baris atas dengan dua dan menolaknya dari yang ketiga. Terima kasih kepada operasi ini, kedua-dua elemen yang kami perlukan dan nombor 4 - elemen lajur kedua baris ketiga - bertukar menjadi sifar.
Kami melihat bahawa sebagai hasil daripada pengurangan itu, matriks segi tiga telah terbentuk. Dalam kes kami, transformasi tidak boleh diteruskan, kerana komponen yang tinggal tidak boleh ditukar kepada sifar.
Jadi, kami menyimpulkan bahawa bilangan baris yang mengandungi nilai berangka dalam matriks ini (atau pangkatnya) ialah 3. Jawapan kepada tugas: 3.
Tugasan 2. Tentukan bilangan baris bebas linear bagi matriks yang diberi.
Kita perlu mencari rentetan sedemikian yang tidak boleh ditukar kepada sifar dengan sebarang transformasi. Malah, kita perlu mencari bilangan baris bukan sifar, atau pangkat matriks yang diwakili. Untuk melakukan ini, mari kita permudahkan.
Kami melihat matriks yang tidak tergolong dalam jenis segi empat sama. Ia mempunyai dimensi 3x4. Mari kita mulakan pelakon juga dari elemen sudut kiri bawah - nombor (-1).
Transformasi lanjut tidak mungkin. Jadi, kami membuat kesimpulan bahawa bilangan garis bebas linear di dalamnya dan jawapan kepada tugas itu ialah 3.
Kini membawa matriks ke bentuk berperingkat bukanlah tugas yang mustahil untuk anda.
Pada contoh tugasan ini, kami menganalisis pengurangan matriks kepada bentuk segi tiga dan bentuk bertingkat. Untuk membatalkan nilai jadual matriks yang dikehendaki, dalam beberapa kes ia diperlukan untuk menunjukkan imaginasi dan mengubah lajur atau barisnya dengan betul. Semoga berjaya dalam matematik dan bekerja dengan matriks!
Walaupun penyelidik biasanya merujuk kepada pengelasan sebagai cara meramalkan kelas objek "tidak diketahui", kami juga boleh menggunakannya untuk menguji ketepatan prosedur pengelasan. Untuk melakukan ini, kami mengambil objek "yang diketahui" (yang kami gunakan dalam terbitan fungsi pengelasan) dan menggunakan peraturan pengelasan kepada mereka. Perkadaran objek yang dikelaskan dengan betul menunjukkan ketepatan prosedur dan secara tidak langsung mengesahkan tahap pemisahan kelas. Jadual, atau "matriks klasifikasi," boleh disediakan untuk menerangkan keputusan. Ini akan membantu kita melihat kesilapan yang lebih kerap dilakukan.
Jadual 12. Matriks pengelasan
Jadual 12 ialah matriks klasifikasi untuk data pengundian Senat. Enam pembolehubah Bardes dengan betul meramalkan taburan puak semua senator (kecuali Capehart) yang gabungan puaknya "dikenali". Ketepatan ramalan dalam kes ini ialah 94.7% (jumlah ramalan yang betul ialah 18 dibahagikan dengan jumlah objek "diketahui"). Kami juga melihat bahawa ralat dalam contoh ini adalah disebabkan oleh pemisahan kumpulan 1 dan 4 yang lemah. Di baris bawah Jadual. 12 menunjukkan taburan mengikut kumpulan objek "tidak diketahui". Ini adalah senator yang Bardes tidak dapat menentukan puaknya daripada data yang dia miliki. Matlamat utamanya ialah menggunakan analisis diskriminasi untuk mengklasifikasikan jawatan senator ini berdasarkan undi mereka, selepas itu dia terus meneroka sikap Senat terhadap pelbagai pilihan untuk bantuan asing.
Peratusan objek "diketahui" yang dikelaskan dengan betul ialah ukuran tambahan perbezaan antara kumpulan. Kami akan menggunakannya, bersama-sama dengan korelasi statistik L umum dan kanonik Wilks, untuk menunjukkan jumlah maklumat diskriminasi yang terkandung dalam pembolehubah. Sebagai ukuran langsung ketepatan ramalan, peratusan ini ialah ukuran maklumat diskriminasi yang paling sesuai. Walau bagaimanapun, nilai peratusan hanya boleh dinilai dengan jangkaan peratusan klasifikasi yang betul apabila pengagihan kepada kelas dibuat secara rawak. Jika terdapat dua kelas, maka dengan pengelasan rawak, 50% ramalan yang betul boleh dijangkakan. Untuk empat kelas, jangkaan ketepatan hanya 25%. Jika untuk dua kelas prosedur pengelasan memberikan 60% ramalan yang betul, maka kecekapannya agak rendah, tetapi untuk empat kelas hasil yang sama menunjukkan kecekapan yang ketara, kerana pengelasan rawak akan memberikan hanya 25% ramalan yang betul. Ini membawa kita kepada statistik -error, yang akan menjadi ukuran prestasi piawai untuk sebarang bilangan kelas:
di mana ialah bilangan objek yang dikelaskan dengan betul, dan ialah kebarangkalian a priori untuk tergolong dalam kelas.
Ungkapan mewakili bilangan objek yang akan diramalkan dengan betul dengan mengelaskannya secara rawak ke dalam kelas mengikut perkadaran dengan kebarangkalian a priori. Jika semua kelas dianggap sama, maka kebarangkalian terdahulu diandaikan sama dengan satu dibahagikan dengan bilangan kelas. Nilai maksimum -statistik ialah 1 dan ia dicapai dalam kes ramalan bebas ralat. Nilai sifar menunjukkan ketidakcekapan prosedur, - statistik juga boleh mengambil nilai negatif, yang menunjukkan diskriminasi yang lemah atau kes yang merosot. Oleh kerana ia mestilah integer, pengangka boleh menjadi negatif semata-mata secara kebetulan, apabila tiada perbezaan antara kelas.
